Σ2333! の 博客
0%

数学分析小思考（广义积分）

发表于 更新于

数学分析小思考（广义积分）

问题背景

周一的习题课，老师讲了一个课后习题，探讨若 \(\displaystyle\int_{a}^{+\infty}{f(x){\rm d}x}\) 收敛，是否就有 \(\lim\limits_{x \to +\infty}{f(x)}=0\) ？然后举了三个反例来论证这个观点是错误的：

反例一

\[ f(x)=\begin{cases}\dfrac{1}{x^2},\qquad x \in \mathbb{R^+}\backslash\mathbb{N^*} \\ n,\qquad x=n \in \mathbb{N^*}\end{cases} \]

首先，在任意区间 \([a,b],\forall a,b>0\) 上，\(f(x)\) 可积

证明（参考证明 \(Riemann\) 函数可积）：

设 \(T\) 是 \([a,b]\) 上的任一分划，\(\{\xi _{k}\}\) 是对应于分划 \(T\) 的任意取定的介点组。作积分和 \[ \sum\limits_{k=1}^{n}{f(\xi_{k}) \Delta x_{k}} \] 因为 \([a,b]\) 中至多有 \([b]-[a]+1\) 个正整数（当 \(b\) 不是整数时，有 \([a]-[b]\) 个正整数；当 \(b\) 是整数时，有 \([a]-[b]+1\) 个正整数），记 \(K=[b]-[a]+1\) ，故在 \([a,b]\) 上满足 \(f(x)>\frac{1}{x^2}\) 的点至多有 \(K\) 个。

所以，对于 \(\forall \varepsilon >0\) ，取 \(\delta = \dfrac{\varepsilon}{2K}>0\) ，则当 \(||T||<\delta\) 时，有 \[ \begin{split} \left|\sum_{k=1}^{n}{f(\xi_{k}) \Delta x_{k} }-\sum_{k=1}^{n}{\frac{1}{ {\xi_{k} }^{2} } \Delta x_{k} }\right| &=\sum_{k=1}^{n}{(f(\xi_{k})-\dfrac{1}{ {\xi_{k} }^{2} }) \Delta x_{k} }\\ &=\sum_{f(x)>\frac{1}{x^2} }{(f(\xi_{k})-\dfrac{1}{ {\xi_{k} }^{2} }) \Delta x_{k} }+\sum_{f(x)\le \frac{1}{x^2} }{(f(\xi_{k})-\dfrac{1}{ {\xi_{k} }^{2} }) \Delta x_{k} }\\ &\le K||T|| + \dfrac{\varepsilon}{2(b-a)}\sum_{k=1}^{n}\Delta x_{k} <\dfrac{\varepsilon}{2}+\dfrac{\varepsilon}{2}=\varepsilon \end{split} \] 由定积分的定义知 \(f(x)\) 函数在 \([a,b]\) 上可积，积分值为 \(\displaystyle\int_{a}^{b}{\frac{1}{x^2}{\rm d}x}=\left.-\frac{1}{x} \ \right|_a^b\)

由无穷积分的定义，\(f(x)\) 都在 \([a,b]\) 上可积，\(\displaystyle\int_{a}^{+\infty}{f(x){\rm d}x}=\lim\limits_{b \to +\infty}{\displaystyle\int_{a}^{b}{f(x){\rm d}x} } = 1\) 收敛

但 \(\lim\limits_{x \to +\infty}{f(x)}=+ \infty\) ，可见 \(\lim\limits_{x \to +\infty}{f(x)} \neq 0\)

反例二

\[ f(x)=sin x^2,x \in [1, +\infty] \]

显然，\(f(x)\) 不收敛，故 \(\lim\limits_{x \to +\infty}{f(x)} \neq 0\)

作换元 \(t=x^2\) ，则当 \(x=1\) 时，\(t=1\) ；当 \(x \to +\infty\) 时，\(t \to +\infty\) ，则 \[ \displaystyle\int_{1}^{+\infty}{f(x){\rm d}x}=\displaystyle\int_{1}^{+\infty}{sin x^2{\rm d}x} =\displaystyle\int_{1}^{+\infty}{\frac{sin t}{2\sqrt{t}}{\rm d}x} \] 显然，\(\displaystyle\int_{1}^{+\infty}{f(x){\rm d}x}\) 收敛

反例三

\[ f(x)=\begin{cases} 2^nx+1-n \cdot 2^n, &x \in [n-\dfrac{1}{2^n},n],\space n \in \mathbb{N^*}\\ -2^nx+1+n \cdot 2^n, &x \in [n, n+\dfrac{1}{2^n}],\space n \in \mathbb{N^*}\\ 0,&x \in [n+\dfrac{1}{2^{n}},n+1-\dfrac{1}{2^{n+1}}] \cup [0,\dfrac{1}{2}],\space n \in \mathbb{N^*} \end{cases} \]

即无穷多个高为\(1\)，底为 \(\dfrac{1}{2^{n-1} }\) 的小三角形

函数图像如图：

img

附上 \(SageMath\) 代码：

1
2
3
4
5
6
7
8
x = var('x')
p = plot(0, (x, 0, 1/2))
for n in range(1,11):
    p0 = plot(0, (x,n+1/2^n, n+1-1/2^(n+1)))
    p1 = plot((2^n * x+1-n*2^n), (x, n-1/2^n, n))
    p2 = plot((-2^n * x+1+n*2^n), (x, n, n+1/2^n))
    p += (p0 + p1 + p2)
show(p)

显然，每个小三角形面积会越来越小并趋于\(0\)，于是 \(\displaystyle\int_{1}^{+\infty}{f(x){\rm d}x}\) 收敛，而 \(\lim\limits_{x \to +\infty}{f(x)} \neq 0\)

条件补充

如课后习题所述，添加了 \(f(x)\) 在 \([a,+\infty)\) 上一致连续的条件后，即当 \(\displaystyle\int_{a}^{+\infty}{f(x){\rm d}x}\) 收敛且 \(f(x)\) 在 \([a,+\infty)\) 上一致连续，则 \(\lim\limits_{x \to +\infty}{f(x)}=0\)

下面给出三种证明方法

证法一（积分上限函数）

因为 \(f(x)\) 在 \([a,+\infty)\) 上一致连续，由一致连续的定义， \(\forall \varepsilon_1>0\)，\(\exists \delta>0\)，\(s.t.\) 当 \(x_1,x_2 \in [a,+\infty)\) 且 \(|x_1-x_2|<\delta\) 时，有 \[ |f(x_1)-f(x_2)|<\dfrac{\varepsilon_1}{2} \]

对于上述 \(\delta\) ，将 \(f(x)\) 表示成积分上限函数 \[ f(x)=\dfrac{1}{\delta}f(x)\displaystyle\int_{x}^{x+\delta}{ {\rm d}t}=\dfrac{1}{\delta}\displaystyle\int_{x}^{x+\delta}{f(x){\rm d}t} \] 所以 \[ \begin{split} |f(x)|&=\dfrac{1}{\delta}|\displaystyle\int_{x}^{x+\delta}{f(x){\rm d}t}|\\ &=\dfrac{1}{\delta}|\displaystyle\int_{x}^{x+\delta}{(f(x)-f(t)){\rm d}t}+\displaystyle\int_{x}^{x+\delta}{f(t){\rm d}t}|\\ &\le \dfrac{1}{\delta}|\displaystyle\int_{x}^{x+\delta}{(f(x)-f(t)){\rm d}t}| + \dfrac{1}{\delta}|\displaystyle\int_{x}^{x+\delta}{f(t){\rm d}t}|\\ &\le \dfrac{1}{\delta}\displaystyle\int_{x}^{x+\delta}{|f(x)-f(t)|{\rm d}t} + \dfrac{1}{\delta}|\displaystyle\int_{x}^{x+\delta}{f(t){\rm d}t}| \end{split} \] 由 \(f(x)\) 一致连续，对于上述 \(\varepsilon_1\)， \[ |f(x)-f(t)|<\dfrac{\varepsilon_1}{2} \] 故 \[ \dfrac{1}{\delta}\displaystyle\int_{x}^{x+\delta}{|f(x)-f(t)|{\rm d}t} <\frac{\varepsilon_1}{2} \] 又因为 \(\displaystyle\int_{a}^{+\infty}{f(x){\rm d}x}\) 收敛，由函数极限的 \(Cauchy\) 收敛准则，\(\forall \varepsilon_2>0\)，\(\exists M>a\)，\(s.t.\) \(\forall x_1,x_2>M\) ，有 \[ |\displaystyle\int_{a}^{x_1}{f(x){\rm d}x}-\displaystyle\int_{a}^{x_2}{f(x){\rm d}x}|<\frac{\varepsilon_2}{2} \] 即 \[ |\displaystyle\int_{x_1}^{x_2}{f(x){\rm d}x}|=|\displaystyle\int_{x_2}^{x_1}{f(x){\rm d}x}|<\frac{\varepsilon_2}{2} \] 故当 \(x\to +\infty\) 时，由 \[ |\displaystyle\int_{x}^{x+\delta}{f(x){\rm d}x}|<\frac{\varepsilon_2}{2} \] 当 \(x\to +\infty\) 时，取 \(\varepsilon = max\{\varepsilon_1,\varepsilon_2\}\) ，对于上述 \(\delta\) ，由 \(\varepsilon_1,\varepsilon_2\) 的任意性，有 \[ |f(x)|\le \dfrac{1}{\delta}\displaystyle\int_{x}^{x+\delta}{|f(x)-f(t)|{\rm d}t} + \dfrac{1}{\delta}|\displaystyle\int_{x}^{x+\delta}{f(t){\rm d}t}|<\frac{\varepsilon_1}{2} + \frac{\varepsilon_2}{2} \le \varepsilon \] 故 \(\lim\limits_{x \to +\infty}{f(x)}=0\) ，得证

证法二（第一积分中值定理）

因为 \(f(x)\) 在 \([a,+\infty)\) 上一致连续，由一致连续的定义， \(\forall \varepsilon>0\)，\(\exists \delta>0\)，\(s.t.\) 当 \(x_1,x_2 \in [a,+\infty)\) 且 \(|x_1-x_2|<\delta\) 时，有 \[ |f(x_1)-f(x_2)|<\dfrac{\varepsilon}{2} \] 对于上述 \(\delta\) ，将无穷积分表示成无穷级数， \[ \displaystyle\int_{a}^{+\infty}{f(x){\rm d}x}=\sum\limits_{n=0}^{\infty}{\displaystyle\int_{a+n\delta}^{a+(n+1)\delta}{f(x){\rm d}x} } \] 根据第一积分中值定理， \(\exists \space \xi_n \in [a+n\delta,a+(n+1)\delta]\) ，\(s.t.\) \[ \displaystyle\int_{a+n\delta}^{a+(n+1)\delta}{f(x){\rm d}x}=f(\xi_n)\displaystyle\int_{a+n\delta}^{a+(n+1)\delta}{ {\rm d}x}=f(\xi_n)\delta,\forall n\in \mathbb{N^*} \] 于是 \[ \displaystyle\int_{a}^{+\infty}{f(x){\rm d}x}=\delta\sum\limits_{n=0}^{\infty}f(\xi_n) \] 因为 \(\displaystyle\int_{a}^{+\infty}{f(x){\rm d}x}\) 收敛，所以 \(\sum\limits_{n=0}^{\infty}f(\xi_n)\) 也收敛

由级数收敛的必要条件，若级数收敛，则其通项收敛于\(0\)，故 \(\lim\limits_{x \to +\infty}{f(\xi_n)}=0\)

即对于上述 \(\varepsilon>0\) ，\(\exists N_1 \in \mathbb{N^*}\) ，\(s.t.\) 当 \(n>N_1\) 时，\(|f(\xi_n)|<\varepsilon\)

又 \(\{\xi_n\}_{n=0}^{\infty}\) 单调递增

对于上述 \(\varepsilon>0\) ，取 \(M = \xi_{N_1+1}\) ，当 \(x>M\) 时，\(\exists N_2>N_1\) ，\(s.t.\) \[ a+N_2\delta \le x \le a+(N_2+1)\delta \] 从而对于上式中的 \(x\)，有 \[ |f(x)|\le |f(x)-f(\xi_{N_2})| + |f(\xi_{N_2})| <\frac{\varepsilon}{2} + \frac{\varepsilon}{2} = \varepsilon \] 故 \(\lim\limits_{x \to +\infty}{f(x)}=0\) ，得证

证法三（反证法）

假设 \(\lim\limits_{x \to \infty}{f(x)} \neq 0\) ，则存在数列 \(\{x_n\}_{n=0}^{\infty}\)，满足 \(\lim\limits_{x \to \infty}{x_n}=+\infty\) ，且 \(\exists \varepsilon_0>0\)， \(\exists N_1 \in \mathbb{N^*}\)，\(s.t.\) 当 \(n>N_1\) 时，\(|f(x_n)|\ge \varepsilon_0\)

因为 \(f(x)\) 在 \([a,+\infty)\) 上一致连续，由一致连续的定义，对于上述 \(\varepsilon_0\)，\(\exists \delta>0\)，\(s.t.\) 当 \(x_1,x_2 \in [a,+\infty)\) 且 \(|x_1-x_2|\le \delta\) 时，有 \[ |f(x_1)-f(x_2)|<\dfrac{\varepsilon_0}{2} \] 于是对于 \(\forall n\in \mathbb{N^*}\)，只要满足 \(|x-x_n|\le \delta\) ，都有 \(|f(x)-f(x_n)|<\dfrac{\varepsilon_0}{2}\)

故 \[ \dfrac{\varepsilon_0}{2}\le f(x_n)-\dfrac{\varepsilon_0}{2}\le f(x) \le f(x_n)+\dfrac{\varepsilon_0}{2} \] 从而 \[ |\displaystyle\int_{x_n-\delta}^{x_n+\delta}{f(x){\rm d}x}|>|\displaystyle\int_{x_n-\delta}^{x_n+\delta}{\dfrac{\varepsilon_0}{2}{\rm d}x}|=\varepsilon_0\delta>0，其中N \in \mathbb{N^*}\cdots\cdots (*) \] 又因为 \(\displaystyle\int_{a}^{+\infty}{f(x){\rm d}x}\) 收敛，由函数极限的 \(Cauchy\) 收敛准则，\(\forall \varepsilon>0\)，\(\exists M>a\)，\(s.t.\) \(\forall x_1,x_2>M\) ，有 \[ |\displaystyle\int_{a}^{x_1}{f(x){\rm d}x}-\displaystyle\int_{a}^{x_2}{f(x){\rm d}x}|<\varepsilon \] 即 \[ |\displaystyle\int_{x_1}^{x_2}{f(x){\rm d}x}|=|\displaystyle\int_{x_2}^{x_1}{f(x){\rm d}x}|<\varepsilon \] 特别地，取 \(\varepsilon=\dfrac{\varepsilon_0\delta}{2}\)，上式也成立

于是由 \(\lim\limits_{x \to \infty}{x_n}=+\infty\) 知， \(\exists N \in \mathbb{N^*}\)，\(s.t.\) 当 \(n>N\) 时，\(x_n-\delta\ge M\)

故 \[ |\displaystyle\int_{x_n-\delta}^{x_n+\delta}{f(x){\rm d}x}| <\dfrac{\varepsilon_0\delta}{2} <\varepsilon_0\delta \] 与 \((*)\) 矛盾

故 \(\lim\limits_{x \to +\infty}{f(x)}=0\) ，得证

拓展猜想

课后，听见隔壁班的同学在讨论这题，认为一致连续（以下简记为条件一）可能是 \(\displaystyle\int_{a}^{+\infty}{f(x){\rm d}x}\) 收敛，则 \(\lim\limits_{x \to \infty}{f(x)}=0\) 的充要条件，即若 \(\displaystyle\int_{a}^{+\infty}{f(x){\rm d}x}\) 收敛，则 \(\lim\limits_{x \to +\infty}{f(x)}=0\) 当且仅当 \(f(x)\) 在 \([a,+\infty)\) 上一致连续

而课后习题还给了另一个条件：设 \(f(x)\) 在 \([a,+\infty)\) 上连续可导，广义积分 \(\displaystyle\int_{a}^{+\infty}{f(x){\rm d}x}\) 和 \(\displaystyle\int_{a}^{+\infty}{f'(x){\rm d}x}\) 都收敛，则 \(\lim\limits_{x \to +\infty}{f(x)}=0\) （以下简记为条件二）

当我指出时（现在想想当时确实有本本主义的感觉），有人反驳道导函数（\(f'(x)\)）有界，不就是 \(f(x)\) 一致连续吗？我当时就被问住了

最初思考

回去想了想，好像可积的必要条件就是被积函数有界噢

由于 \(\displaystyle\int_{a}^{+\infty}{f'(x){\rm d}x}\) 收敛，所以 \(f'(x)\) 必定可积，即 \(\exists M\ge 0\)，\(s.t.\forall x\ge a\)， \(|f'(x)|\ge M\)

则 \(\forall x_1,x_2\ge a\) ，有 \[ |f(x_1)-f(x_2)|\le M|x_1-x_2| \] 满足 \(Lipschitz\) 条件

\(Lipschitz\) 条件其实是强于一致收敛的，这里给出由 \(Lipschitz\) 条件推出一致收敛的证明：

\(\forall \varepsilon>0\)，取 \(\delta = \dfrac{\varepsilon}{2M}\) ，\(s.t.\) 当 \(\forall x_1,x_2\ge a\) 且 \(|x_1-x_2|<\delta\) 时，有 \[ |f(x_1)-f(x_2)|\le M|x_1-x_2|= \dfrac{\varepsilon}{2} < \varepsilon \] 证毕（是不是非常简单？）

这样就回到了一致连续的条件

质疑

当然，我的自尊心告诉我不能就此放弃

首先，我们知道，对于定义域为闭区间的定积分，被积函数有界是函数可积的必要条件，这是毋庸置疑的

然而，对于无穷积分，是否仍然有这样的性质呢？

容易发现反例一中的函数显然是无界的（虽然不是连续的），基本上能否定由于 \(\displaystyle\int_{a}^{+\infty}{f'(x){\rm d}x}\) 收敛则 \(f'(x)\) 必定有界了

而且，对于广义积分，如果被积函数都有界，那就不存在瑕点的定义了

瑕点的定义为：被积函数在区间上没有定义且其附近无界的点

所以可以否定 \(f'(x)\) 必定有界

弯路

尽管如此，但我们只否认了由 \(\displaystyle\int_{a}^{+\infty}{f'(x){\rm d}x}\) 收敛推出 \(f'(x)\) 必定有界，再有 \(Lipschitz\) 条件推出一致连续来证明的这条路

仍然无法充分说明一致连续不是充要条件

那么，如果我们能够找到一个函数满足条件二，但不满足条件一（一致连续），那么就能说明一致连续不是充要条件了

我想了挺久，用了 \(sin\dfrac{1}{x}\) 之类的恶心的函数，但没有找到合适的函数同时满足：在 \([a,+\infty)\) 上连续可导，广义积分 \(\displaystyle\int_{a}^{+\infty}{f(x){\rm d}x}\) 和 \(\displaystyle\int_{a}^{+\infty}{f'(x){\rm d}x}\) 都收敛

正当我要放弃时，我看到了反例三，于是灵光一现：

欸，如果我不能让 \(f(x)\) 收敛，为什么我不能让 \(dx\) 收敛呢？

于是我构造了这样的函数： \[ g(x)=\begin{cases} n\cdot 2^nx+n-n^2 \cdot 2^n, &x \in [n-\dfrac{1}{2^n},n],\space n \in \mathbb{N^*}\\ -n\cdot 2^nx+n+n^2 \cdot 2^n, &x \in [n, n+\dfrac{1}{2^n}],\space n \in \mathbb{N^*}\\ 0,&x \in [n+\dfrac{1}{2^{n}},n+1-\dfrac{1}{2^{n+1}}] \cup [0,\dfrac{1}{2}],\space n \in \mathbb{N^*} \end{cases} \] 即无穷多个高为\(n\)，底为 \(\dfrac{1}{2^{n-1} }\) 的小三角形

则每个小三角形的面积 \(s_n=\dfrac{n}{2^{n} }\) ，显然，\(\lim\limits_{n\to \infty}{s_n} = 0\) （用 \(Heine\) 定理和 \(L'Hospital\) 法则容易证明，或者你可以用其他方法，这里不再赘述）

由 \(Cauchy\) 检根法，\(\sqrt[n]{\dfrac{n}{2^{n} } }=\dfrac{1}{2}\) ，所以 \(\sum\limits_{n=1}^{\infty}{\dfrac{n}{2^{n} } }\) 收敛

因此，\(\displaystyle\int_{a}^{+\infty}{g(x){\rm d}x}\) 收敛

函数图像如图所示：

img

附上 \(SageMath\) 代码：

1
2
3
4
5
6
7
8
x = var('x')
p = plot(0, (x, 0, 1/2))
for n in range(1,11):
    p0 = plot(0, (x,n+1/2^n, n+1-1/2^(n+1)))
    p1 = plot((n * 2^n * x+n-n^2 * 2^n), (x, n-1/2^n, n))
    p2 = plot((-n * 2^n * x+n+n^2 * 2^n), (x, n, n+1/2^n))
    p += (p0 + p1 + p2)
show(p)

构造一

令 \(f'(x)=g(x)\)，则 \[ f(x)=\begin{cases} n\cdot 2^{n-1}x^2+(n-n^2 \cdot 2^n)x+C, &x \in [n-\dfrac{1}{2^n},n],\space n \in \mathbb{N^*}\\ -n\cdot 2^{n-1}x^2+(n+n^2 \cdot 2^n)x+C, &x \in [n, n+\dfrac{1}{2^n}],\space n \in \mathbb{N^*}\\ C,&x \in [n+\dfrac{1}{2^{n}},n+1-\dfrac{1}{2^{n+1}}] \cup [0,\dfrac{1}{2}],\space n \in \mathbb{N^*} \end{cases} \] 为了使 \(\displaystyle\int_{a}^{+\infty}{f(x){\rm d}x}\) 收敛，令 \(C=0\)

函数图像如图所示：

img

附上 \(SageMath\) 代码：

1
2
3
4
5
6
7
8
x = var('x')
p = plot(0, (x, 0, 1/2))
for n in range(1,3):
    p0 = plot(0, (x,n+1/2^n, n+1-1/2^(n+1)))
    p1 = plot((n * 2^(n-1) * x^2 + (n-n^2 * 2^n)*x), (x, n-1/2^n, n))
    p2 = plot((-n * 2^(n-1) * x^2 + (n+n^2 * 2^n)*x), (x, n, n+1/2^n))
    p += (p0 + p1 + p2)
show(p)

啊这

构造出的 \(f(x)\) 不连续

构造二

虽然构造一失败了，但是给了我启发：原本是想由于 \(g(x)\) 与三角形顶点处不可导，就令 \(f'(x)=g(x)\)，那不妨对 \(g(x)\) 进行修正，记为 \(h(x)\)，然后令 \(f(x)=h(x)\)

尝试用二次函数来修正 \(g(x)\) ，分成三段： \[ y_1=(x+\dfrac{1}{2^n})^2\\ y_2=-x^2+n\\ y_3=(x-\dfrac{1}{2^n})^2 \] 然后我们来限定区间，仅在区间 \([n-\dfrac{1}{2^n},n+\dfrac{1}{2^n}],\) 讨论即可，之后进行平移操作

为了使函数连续可导，得到 \[ h(x)=\begin{cases} (x-n+\dfrac{1}{2^n})^2, &x \in [n-\dfrac{1}{2^n},n-\dfrac{1}{2^{n+1}}],\space n \in \mathbb{N^*}\\ -(x-n)^2+n, &x \in [n-\dfrac{1}{2^{n+1}}, n+\dfrac{1}{2^{n+1}}],\space n \in \mathbb{N^*}\\ (x-n-\dfrac{1}{2^n})^2, &x \in [n+\dfrac{1}{2^{n+1}},n-\dfrac{1}{2^n}],\space n \in \mathbb{N^*}\\ 0,&x \in [n+\dfrac{1}{2^{n}},n+1-\dfrac{1}{2^{n+1}}] \cup [0,\dfrac{1}{2}],\space n \in \mathbb{N^*} \end{cases} \] 函数图像如图所示：

img

附上 \(SageMath\) 代码：

1
2
3
4
5
6
7
8
9
x = var('x')
p = plot(0, (x, 0, 1/2))
for n in range(1,3):
    p0 = plot(0, (x,n+1/2^n, n+1-1/2^(n+1)))
    p1 = plot((x-n + 1/2^n)^2, (x, n-1/2^n, n-1/2^(n+1)))
    p2 = plot((-(x-n)^2+n), (x, n-1/2^(n+1), n+1/2^(n+1)))
    p3 = plot((x-n - 1/2^n)^2, (x, n+1/2^(n+1), n+1/2^n))
    p += (p0 + p1 + p2 + p3)
show(p)

显然这不连续

构造三

还不死心，继续构造

为解决构造二中间段的问题，增加一个参数 \(k\) ，类似于构造二，分三段 \[ y_1=(kx+\dfrac{1}{2^n})^2\\ y_2=-(kx)^2+n\\ y_3=(kx-\dfrac{1}{2^n})^2 \] 为使连接处连续可导，联立方程组 \[ \begin{cases} &y_1=y_2\\ &y_1'=y_2' \end{cases} \] 解得 \[ \begin{cases} &x=\dfrac{1}{2^{n+1}}\\ &k=\pm \sqrt{n\cdot 2^{2n+1}-1} -1 \end{cases} \] 将 \(k=\sqrt{n\cdot 2^{2n+1}-1} -1\) 代入得 \[ h(x)=\begin{cases} ((\sqrt{n\cdot 2^{2n+1}-1} -1)(x-n)+\dfrac{1}{2^n})^2, &x \in [n-\dfrac{1}{2^n},n-\dfrac{1}{2^{n+1}}],\space n \in \mathbb{N^*}\\ -[(\sqrt{n\cdot 2^{2n+1}-1} -1)(x-n)]^2+n, &x \in [n-\dfrac{1}{2^{n+1}}, n+\dfrac{1}{2^{n+1}}],\space n \in \mathbb{N^*}\\ ((\sqrt{n\cdot 2^{2n+1}-1} -1)(x-n)-\dfrac{1}{2^n})^2, &x \in [n+\dfrac{1}{2^{n+1}},n-\dfrac{1}{2^n}],\space n \in \mathbb{N^*}\\ 0,&x \in [n+\dfrac{1}{2^{n}},n+1-\dfrac{1}{2^{n+1}}] \cup [0,\dfrac{1}{2}],\space n \in \mathbb{N^*} \end{cases} \] 显然，当 \(n=1\) 时就不对了

img

附上 \(SageMath\) 代码：

1
2
3
4
5
x = var('x')
p = plot(0, (x, 0, 1/2))
n=1
p1 = plot((sqrt(n*2^(2*n+1)-1)*(x-n) + 1/2^n)^2, (x, n-1/2^n, n-1/2^(n+1)))
show(p+p1)

又出现了 \(0\) 与第一段函数之间的间断点

也不是我们要的答案

理论推导

忙活了半天，什么结论也没有得出来

我们只能说，构造出满足在 \([a,+\infty)\) 上连续可导，广义积分 \(\displaystyle\int_{a}^{+\infty}{f(x){\rm d}x}\) 和 \(\displaystyle\int_{a}^{+\infty}{f'(x){\rm d}x}\) 都收敛，且不一致连续的函数是困难的

而当我们转向理论时，会发现其实是非常明了的

对于条件二，

因为 \(\displaystyle\int_{a}^{+\infty}{f'(x){\rm d}x}=\lim\limits_{x\to +\infty}{f(x)}-f(a)\)

由 \(\displaystyle\int_{a}^{+\infty}{f'(x){\rm d}x}\) 收敛可得 \(\lim\limits_{x\to +\infty}{f(x)}\) 收敛，即 \(f(x)\) 在 \([a,+\infty)\) 上极限存在

设 \(\lim\limits_{x\to +\infty}{f(x)}=A\)

则对于 \(\forall \varepsilon>0\)，\(\exists M>max\{a, 0\}\)，\(s.t.\) 当 \(x>M\) 时， \[ |f(x)-A|<\dfrac{\varepsilon}{2} \]

对于上述 \(\varepsilon\)，\(\exists \delta>0\)，\(s.t. \forall x_1,x_2\in [M+1,+\infty)\) 且 \(|x_1-x_2|<\delta\) ，有 \[ |f(x_1)-f(x_2)|\le|f(x_1)-A|+|f(x_2)-A|<\dfrac{\varepsilon}{2}+\dfrac{\varepsilon}{2}=\varepsilon \]

又 \(f(x)\) 在 \([a,+\infty)\) 上连续

由连续函数在闭区间上的一致连续性可得，\(f(x)\) 在 \([a,M+1]\) 一致连续

故 \(f(x)\) 在 \([a,+\infty)\) 上一致连续

条件二转化成了条件一

条件讨论

我们最终得到，条件一和条件二是等价的，那么是否说明 \(f(x)\) 一致连续就是 \(\displaystyle\int_{a}^{+\infty}{f(x){\rm d}x}\) 收敛，则 \(\lim\limits_{x \to +\infty}{f(x)}=0\) 的充要条件呢？

其实不然

连续性条件

我们推导了若 \(\displaystyle\int_{a}^{+\infty}{f(x){\rm d}x}\) 收敛，\(f(x)\) 一致连续，则 \(\lim\limits_{x \to +\infty}{f(x)}=0\)

即若 \(\displaystyle\int_{a}^{+\infty}{f(x){\rm d}x}\) 收敛，\(f(x)\) 一致连续 \(\Rightarrow\) \(\lim\limits_{x \to +\infty}{f(x)}=0\)

而若 \(\displaystyle\int_{a}^{+\infty}{f(x){\rm d}x}\) 收敛， \(\lim\limits_{x \to +\infty}{f(x)}=0\) ，当 \(f(x)\) 不是连续函数时，则 \(f(x)\) 显然不一致连续

例如，构造函数 \(f(x)=\dfrac{1}{[x]}\)

函数图像如图所示：

img

附上 \(SageMath\) 代码：

1
2
3
4
5
x = var('x')
p = plot(1, (x, 1, 2))
for n in range(2, 50):
    p += plot(1/n, (x, n, n+1))
show(p)

故当 \(f(x)\) 是 \([a,+\infty)\) 上的连续函数时，若 \(\displaystyle\int_{a}^{+\infty}{f(x){\rm d}x}\) 收敛， \(\lim\limits_{x \to +\infty}{f(x)}=0\) ，则 \(f(x)\) 一致连续，但此时 \(\displaystyle\int_{a}^{+\infty}{f(x){\rm d}x}\) 收敛的条件就多余了

即若 \(f(x)\) 是 \([a,+\infty)\) 上的连续函数， \(\lim\limits_{x \to +\infty}{f(x)}=0\Rightarrow f(x)\) 一致连续

综上所述，若 \(f(x)\) 是 \([a,+\infty)\) 上的连续函数且 \(\displaystyle\int_{a}^{+\infty}{f(x){\rm d}x}\) 收敛，则 \(\lim\limits_{x \to +\infty}{f(x)}=0\) 当且仅当 \(f(x)\) 一致连续。 \(f(x)\) 是 \([a,+\infty)\) 上的连续函数与 \(\displaystyle\int_{a}^{+\infty}{f(x){\rm d}x}\) 收敛缺少任何一个条件，充要条件均不成立

单调性条件

除了连续性，考察一个函数另一个重要的性质就是单调性

设函数 \(f(x)\) 在 \([a, +\infty)\) 上单调，且 \(\displaystyle\int_{a}^{+\infty}{f(x){\rm d}x}\) 收敛，是否可以推出， \(\lim\limits_{x \to +\infty}{f(x)}=0\) ？

不妨设 \(f(x)\) 在 \([a, +\infty)\) 上单调递减

若 \(\exists x_0>a\)，\(s.t.\) 当 \(x>x_0\) 时，\(f(x)<0\) ，则 \(\exists \delta>0\)，\(s.t.f(x_0 + \delta)<0\) ，故 \[ \displaystyle\int_{a}^{+\infty}{f(x){\rm d}x}=\displaystyle\int_{a}^{x_0 + \delta}{f(x){\rm d}x}+\displaystyle\int_{x_0 + \delta}^{+\infty}{f(x){\rm d}x}<\displaystyle\int_{a}^{x_0 + \delta}{f(x){\rm d}x}+\lim\limits_{w\to +\infty}f(x_0 + \delta)[w-(x_0 + \delta)] = -\infty \] 显然 \(\displaystyle\int_{a}^{+\infty}{f(x){\rm d}x}\) 不收敛，矛盾

若 \(f(x)\) 在 \([a, +\infty)\) 上非负，且 \(\lim\limits_{x \to \infty}{f(x)}=A>0\) ，则 \[ \displaystyle\int_{a}^{+\infty}{f(x){\rm d}x}>\lim\limits_{w\to +\infty}A(w-a)=+\infty \] 显然 \(\displaystyle\int_{a}^{+\infty}{f(x){\rm d}x}\) 也不收敛，矛盾

所以， \(\lim\limits_{x \to +\infty}{f(x)}=0\)

事实上，我们可以根据单调性条件推出更强的条件：

设函数 \(f(x)\) 在 \([a, +\infty)\) 上单调，且 \(\displaystyle\int_{a}^{+\infty}{f(x){\rm d}x}\) 收敛， \(\lim\limits_{x \to +\infty}{xf(x)}=0\) ，即 \(f(x) \sim o(\dfrac{1}{x})(x\to +\infty)\)

不妨设 \(f(x)\) 在 \([a, +\infty)\) 上单调递减，由上述分析可得， \(f(x)\) 在 \([a, +\infty)\) 上非负，且 \(\lim\limits_{x \to +\infty}{f(x)}=0\)

类似于条件补充中的证法一，构造积分上限函数 \(\displaystyle\int_{\frac{x}{2} }^{x}{f(x){\rm d}t}\) ，其中 \(\dfrac{x}{2}\ge a\)，则有 \[ 0\le \dfrac{1}{2}xf(x) =\displaystyle\int_{\frac{x}{2}}^{x}{f(x){\rm d}t} \] 由 \(f(x)\) 的单调性，\(\forall t\in [\dfrac{x}{2}, x]\)，有 \(f(t)\ge f(x)\) ，故 \[ \displaystyle\int_{\frac{x}{2}}^{x}{f(x){\rm d}t}\le \displaystyle\int_{\frac{x}{2}}^{x}{f(t){\rm d}t} \] 又 \(\displaystyle\int_{a}^{+\infty}{f(x){\rm d}x}\) 收敛，由函数极限的 \(Cauchy\) 收敛准则，\(\forall \varepsilon>0\)，\(\exists M>a\)，\(s.t.\) \(\forall x>M\) ，有 \[ \displaystyle\int_{a}^{+\infty}{f(x){\rm d}x} < \varepsilon \] 故对于上述 \(\varepsilon\)，有 \[ 0\le \lim\limits_{x \to +\infty}\dfrac{1}{2}xf(x) =\lim\limits_{x \to +\infty}\displaystyle\int_{\frac{x}{2}}^{x}{f(x){\rm d}t}\le \lim\limits_{x \to +\infty}\displaystyle\int_{\frac{x}{2}}^{x}{f(t){\rm d}t} < \varepsilon \] 故 \(\lim\limits_{x \to +\infty}{xf(x)}=0\)

显然，由单调性条件得出的结论是强于连续性条件得出的结论的，我们基本可以认定单调性是非必要的

类似于反例一，构造函数 \[ f(x)=\begin{cases}\dfrac{1}{x^2},\qquad x \in \mathbb{R^+}\backslash\mathbb{N^*} \\ \dfrac{1}{x},\qquad x=n \in \mathbb{N^*}\end{cases} \] 显然， \(\displaystyle\int_{a}^{+\infty}{f(x){\rm d}x}\) 收敛，且 \(\lim\limits_{x \to +\infty}{f(x)}=0\) ，而 \(f(x)\) 是非单调的

可导条件

另外，注意到条件二中的可导条件，我们再讨论一下可导是否是必要的

类比于反例三，我们可以构造这样的函数： \[ f(x)=\begin{cases} \dfrac{2^n}{n}x-2^n+\dfrac{1}{n}, &x \in [n-\dfrac{1}{2^n},n],\space n \in \mathbb{N^*}\\ -\dfrac{2^n}{n}x+2^n+\dfrac{1}{n}, &x \in [n, n+\dfrac{1}{2^n}],\space n \in \mathbb{N^*}\\ 0,&x \in [n+\dfrac{1}{2^{n}},n+1-\dfrac{1}{2^{n+1}}] \cup [0,\dfrac{1}{2}],\space n \in \mathbb{N^*} \end{cases} \] 函数图像如图所示：

img

附上 \(SageMath\) 代码：

1
2
3
4
5
6
7
8
x = var('x')
p = plot(0, (x, 0, 1/2))
for n in range(1,11):
    p0 = plot(0, (x,n+1/2^n, n+1-1/2^(n+1)))
    p1 = plot((1/n * 2^n * x - 2^n + 1/n), (x, n-1/2^n, n))
    p2 = plot((-1/n * 2^n * x+ 2^n + 1/n), (x, n, n+1/2^n))
    p += (p0 + p1 + p2)
show(p)

显然，\(f(x)\) 在三角形的顶点处均不可导，而 \(f(x)\) 是连续函数， \(\displaystyle\int_{a}^{+\infty}{f(x){\rm d}x}\) 收敛， \(\lim\limits_{x \to \infty}{f(x)}=0\) ，且 \(f(x)\) 一致连续

特别地，一些特殊的函数，处处连续，处处不可导

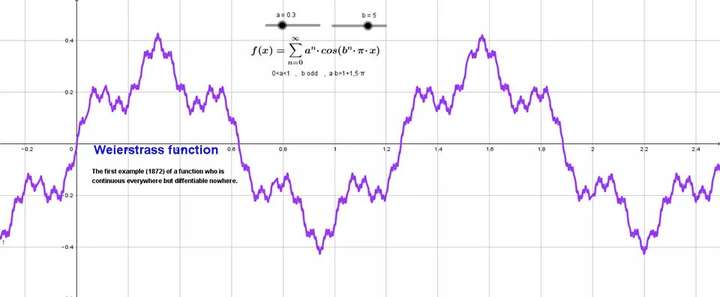
这里以著名的 \(Weierstrass\) 函数为例（这是第一个被发现的处处连续但处处不可导的函数，这个函数以及它处处连续而又处处不可导的证明首次出现在魏尔施特拉斯于1872年7月18日在普鲁士科学院出版的一篇论文中）

魏尔施特拉斯的原作中给出的构造是： \[ f(x)=\sum\limits_{n=0}^{+\infty}{a^ncos(b^{n}\pi x)} \]

其中 \(0<a<1\)，\(b\) 为正奇数，\(s.t.ab>1+\dfrac{3}{2}\pi\)

其函数图像如图所示：

img

鸣谢

感谢隔壁班的同学们，在给予我灵感与思想的火花

感谢我的同学们，在我走弯路是给予的帮助与纠正

欢迎关注我的其它发布渠道

-------- 本文结束 感谢阅读 --------