BUUCTF 每日打卡 2021-8-13
引言
无
[羊城杯 2020]RRRRRRRSA
加密代码如下：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
| import sympy
from Crypto.Util.number import *
flag = 'GWHT{************}'
flag1 = flag[:19].encode()
flag2 = flag[19:].encode()
assert(len(flag) == 38)
P1 = getPrime(1038)
P2 = sympy.nextprime(P1)
assert(P2 - P1 < 1000)
Q1 = getPrime(512)
Q2 = sympy.nextprime(Q1)
N1 = P1 * P1 * Q1
N2 = P2 * P2 * Q2
E1 = getPrime(1024)
E2 = sympy.nextprime(E1)
m1 = bytes_to_long(flag1)
m2 = bytes_to_long(flag2)
c1 = pow(m1, E1, N1)
c2 = pow(m2, E2, N2)
output = open('secret', 'w')
output.write('N1=' + str(N1) + '\n')
output.write('c1=' + str(c1) + '\n')
output.write('E1=' + str(E1) + '\n')
output.write('N2=' + str(N2) + '\n')
output.write('c2=' + str(c2) + '\n')
output.write('E2=' + str(E2) + '\n')
output.close()
|
secret如下：
1
2
3
4
5
6
| N1=60143104944034567859993561862949071559877219267755259679749062284763163484947626697494729046430386559610613113754453726683312513915610558734802079868190554644983911078936369464590301246394586190666760362763580192139772729890492729488892169933099057105842090125200369295070365451134781912223048179092058016446222199742919885472867511334714233086339832790286482634562102936600597781342756061479024744312357407750731307860842457299116947352106025529309727703385914891200109853084742321655388368371397596144557614128458065859276522963419738435137978069417053712567764148183279165963454266011754149684758060746773409666706463583389316772088889398359242197165140562147489286818190852679930372669254697353483887004105934649944725189954685412228899457155711301864163839538810653626724347
c1=55094296873556883585060020895253176070835143350249581136609315815308788255684072804968957510292559743192424646169207794748893753882418256401223641287546922358162629295622258913168323493447075410872354874300793298956869374606043622559405978242734950156459436487837698668489891733875650048466360950142617732135781244969524095348835624828008115829566644654403962285001724209210887446203934276651265377137788183939798543755386888532680013170540716736656670269251318800501517579803401154996881233025210176293554542024052540093890387437964747460765498713092018160196637928204190194154199389276666685436565665236397481709703644555328705818892269499380797044554054118656321389474821224725533693520856047736578402581854165941599254178019515615183102894716647680969742744705218868455450832
E1=125932919717342481428108392434488550259190856475011752106073050593074410065655587870702051419898088541590032209854048032649625269856337901048406066968337289491951404384300466543616578679539808215698754491076340386697518948419895268049696498272031094236309803803729823608854215226233796069683774155739820423103
N2=60143104944034567859993561862949071559877219267755259679749062284763163484947626697494729046430386559610613113754453726683312513915610558734802079868195633647431732875392121458684331843306730889424418620069322578265236351407591029338519809538995249896905137642342435659572917714183543305243715664380787797562011006398730320980994747939791561885622949912698246701769321430325902912003041678774440704056597862093530981040696872522868921139041247362592257285423948870944137019745161211585845927019259709501237550818918272189606436413992759328318871765171844153527424347985462767028135376552302463861324408178183842139330244906606776359050482977256728910278687996106152971028878653123533559760167711270265171441623056873903669918694259043580017081671349232051870716493557434517579121
c2=39328446140156257571484184713861319722905864197556720730852773059147902283123252767651430278357950872626778348596897711320942449693270603776870301102881405303651558719085454281142395652056217241751656631812580544180434349840236919765433122389116860827593711593732385562328255759509355298662361508611531972386995239908513273236239858854586845849686865360780290350287139092143587037396801704351692736985955152935601987758859759421886670907735120137698039900161327397951758852875291442188850946273771733011504922325622240838288097946309825051094566685479503461938502373520983684296658971700922069426788236476575236189040102848418547634290214175167767431475003216056701094275899211419979340802711684989710130215926526387138538819531199810841475218142606691152928236362534181622201347
E2=125932919717342481428108392434488550259190856475011752106073050593074410065655587870702051419898088541590032209854048032649625269856337901048406066968337289491951404384300466543616578679539808215698754491076340386697518948419895268049696498272031094236309803803729823608854215226233796069683774155739820425393
|
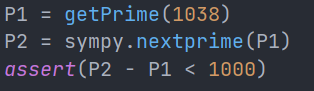
刚拿到题目时注意到： ![在这里插入图片描述]()
想着能不能利用这个条件把P1,P2爆破出来，后来发现数字太大不好爆破 又看这个E1,E2很大，能不能用wiener attack（你要忍一下），结果网上找到脚本解不出来 然后就想干脆直接爆破N1, N2吧，就试着factordb了一下，结果： ![在这里插入图片描述]()
笑死 花里胡哨，一拳打死 然后就是RSA解密，和平常不同的是，N由三个素数相乘，怎么计算φ 可以参考这篇欧拉函数的计算式 ![在这里插入图片描述]()
解密代码如下：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
| import sympy
from Crypto.Util.number import *
N1 = 60143104944034567859993561862949071559877219267755259679749062284763163484947626697494729046430386559610613113754453726683312513915610558734802079868190554644983911078936369464590301246394586190666760362763580192139772729890492729488892169933099057105842090125200369295070365451134781912223048179092058016446222199742919885472867511334714233086339832790286482634562102936600597781342756061479024744312357407750731307860842457299116947352106025529309727703385914891200109853084742321655388368371397596144557614128458065859276522963419738435137978069417053712567764148183279165963454266011754149684758060746773409666706463583389316772088889398359242197165140562147489286818190852679930372669254697353483887004105934649944725189954685412228899457155711301864163839538810653626724347
c1 = 55094296873556883585060020895253176070835143350249581136609315815308788255684072804968957510292559743192424646169207794748893753882418256401223641287546922358162629295622258913168323493447075410872354874300793298956869374606043622559405978242734950156459436487837698668489891733875650048466360950142617732135781244969524095348835624828008115829566644654403962285001724209210887446203934276651265377137788183939798543755386888532680013170540716736656670269251318800501517579803401154996881233025210176293554542024052540093890387437964747460765498713092018160196637928204190194154199389276666685436565665236397481709703644555328705818892269499380797044554054118656321389474821224725533693520856047736578402581854165941599254178019515615183102894716647680969742744705218868455450832
E1 = 125932919717342481428108392434488550259190856475011752106073050593074410065655587870702051419898088541590032209854048032649625269856337901048406066968337289491951404384300466543616578679539808215698754491076340386697518948419895268049696498272031094236309803803729823608854215226233796069683774155739820423103
N2 = 60143104944034567859993561862949071559877219267755259679749062284763163484947626697494729046430386559610613113754453726683312513915610558734802079868195633647431732875392121458684331843306730889424418620069322578265236351407591029338519809538995249896905137642342435659572917714183543305243715664380787797562011006398730320980994747939791561885622949912698246701769321430325902912003041678774440704056597862093530981040696872522868921139041247362592257285423948870944137019745161211585845927019259709501237550818918272189606436413992759328318871765171844153527424347985462767028135376552302463861324408178183842139330244906606776359050482977256728910278687996106152971028878653123533559760167711270265171441623056873903669918694259043580017081671349232051870716493557434517579121
c2 = 39328446140156257571484184713861319722905864197556720730852773059147902283123252767651430278357950872626778348596897711320942449693270603776870301102881405303651558719085454281142395652056217241751656631812580544180434349840236919765433122389116860827593711593732385562328255759509355298662361508611531972386995239908513273236239858854586845849686865360780290350287139092143587037396801704351692736985955152935601987758859759421886670907735120137698039900161327397951758852875291442188850946273771733011504922325622240838288097946309825051094566685479503461938502373520983684296658971700922069426788236476575236189040102848418547634290214175167767431475003216056701094275899211419979340802711684989710130215926526387138538819531199810841475218142606691152928236362534181622201347
E2 = 125932919717342481428108392434488550259190856475011752106073050593074410065655587870702051419898088541590032209854048032649625269856337901048406066968337289491951404384300466543616578679539808215698754491076340386697518948419895268049696498272031094236309803803729823608854215226233796069683774155739820425393
P1 = 2274225198252001349705635635570523977229824105257244100474886998299874359980121470818908135119780772090534507154122446275044273088642034569778714650980895003300783785404556303992237495059194352539844239687490397036174178433587393753764414486675415691276936408808667228951877003555601842900641222777857711016758899
Q1 = 11628371843051760370952910026406764366191062991235308941262037248377376991693250742343307155422036713746576338866595433599862614339347536916226536644210947
P2 = sympy.nextprime(P1)
Q2 = sympy.nextprime(Q1)
phi1 = P1 * (P1 - 1) * (Q1 - 1)
phi2 = P2 * (P2 - 1) * (Q2 - 1)
d1 = inverse(E1, phi1)
d2 = inverse(E2, phi2)
m1 = pow(c1, d1, N1)
m2 = pow(c2, d2, N2)
print(long_to_bytes(m1) + long_to_bytes(m2))
|
结果为： ![在这里插入图片描述]()
如果真的是这么解的话那就太草了，就去找了找大佬的解法，采用了连分数,低解密指数攻击原理 RSA中有一个很著名的攻击方法，低解密指数攻击，其中的代表就是wiener attack 其中就用到了连分数，具体原理网上都有，这里不再赘述 唯一令我疑惑的是，为什么可以用连分数，并且保证有解（这在很多介绍维纳攻击法的文章中是没有提到或者一笔带过的），我找到了一篇介绍wiener attack的论文，有这样一段话： ![在这里插入图片描述]()
然后我去搜了关于连分数的勒让德理论，找到了另一篇论文，给出了证明： ![在这里插入图片描述]()
关于维纳攻击法的完整推导，我打算出一期完整的博客 关于本题，由于 \[
\dfrac{N1}{N2} = \left(\dfrac{P1}{P2}\right)^{2}\left(\dfrac{Q1}{Q2}\right)
\] 又因为有P2 = sympy.nextprime(P1)，Q2 = sympy.nextprime(Q1)且\(P2-P1<1000\) 所以有\(\dfrac{Q1}{Q2} < \dfrac{N1}{N2}\)且\(\dfrac{P1}{P2} \approx 1\)，\(\dfrac{Q1}{Q2} \to 1\) 但是不能确定是否满足条件： \[
\left| \dfrac{N1}{N2}-\dfrac{Q1}{Q2}\right| = \left[ \left(\dfrac{P1}{P2} - 1\right)^{2}\right] \left(\dfrac{Q1}{Q2}\right)<\dfrac{1}{2(Q2)^{2}}
\] 可能也是通过猜测得到的解法吧 对wp的代码作了一些修改：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
| import gmpy2
from Crypto.Util.number import *
N1 = 60143104944034567859993561862949071559877219267755259679749062284763163484947626697494729046430386559610613113754453726683312513915610558734802079868190554644983911078936369464590301246394586190666760362763580192139772729890492729488892169933099057105842090125200369295070365451134781912223048179092058016446222199742919885472867511334714233086339832790286482634562102936600597781342756061479024744312357407750731307860842457299116947352106025529309727703385914891200109853084742321655388368371397596144557614128458065859276522963419738435137978069417053712567764148183279165963454266011754149684758060746773409666706463583389316772088889398359242197165140562147489286818190852679930372669254697353483887004105934649944725189954685412228899457155711301864163839538810653626724347
c1 = 55094296873556883585060020895253176070835143350249581136609315815308788255684072804968957510292559743192424646169207794748893753882418256401223641287546922358162629295622258913168323493447075410872354874300793298956869374606043622559405978242734950156459436487837698668489891733875650048466360950142617732135781244969524095348835624828008115829566644654403962285001724209210887446203934276651265377137788183939798543755386888532680013170540716736656670269251318800501517579803401154996881233025210176293554542024052540093890387437964747460765498713092018160196637928204190194154199389276666685436565665236397481709703644555328705818892269499380797044554054118656321389474821224725533693520856047736578402581854165941599254178019515615183102894716647680969742744705218868455450832
E1 = 125932919717342481428108392434488550259190856475011752106073050593074410065655587870702051419898088541590032209854048032649625269856337901048406066968337289491951404384300466543616578679539808215698754491076340386697518948419895268049696498272031094236309803803729823608854215226233796069683774155739820423103
N2 = 60143104944034567859993561862949071559877219267755259679749062284763163484947626697494729046430386559610613113754453726683312513915610558734802079868195633647431732875392121458684331843306730889424418620069322578265236351407591029338519809538995249896905137642342435659572917714183543305243715664380787797562011006398730320980994747939791561885622949912698246701769321430325902912003041678774440704056597862093530981040696872522868921139041247362592257285423948870944137019745161211585845927019259709501237550818918272189606436413992759328318871765171844153527424347985462767028135376552302463861324408178183842139330244906606776359050482977256728910278687996106152971028878653123533559760167711270265171441623056873903669918694259043580017081671349232051870716493557434517579121
c2 = 39328446140156257571484184713861319722905864197556720730852773059147902283123252767651430278357950872626778348596897711320942449693270603776870301102881405303651558719085454281142395652056217241751656631812580544180434349840236919765433122389116860827593711593732385562328255759509355298662361508611531972386995239908513273236239858854586845849686865360780290350287139092143587037396801704351692736985955152935601987758859759421886670907735120137698039900161327397951758852875291442188850946273771733011504922325622240838288097946309825051094566685479503461938502373520983684296658971700922069426788236476575236189040102848418547634290214175167767431475003216056701094275899211419979340802711684989710130215926526387138538819531199810841475218142606691152928236362534181622201347
E2 = 125932919717342481428108392434488550259190856475011752106073050593074410065655587870702051419898088541590032209854048032649625269856337901048406066968337289491951404384300466543616578679539808215698754491076340386697518948419895268049696498272031094236309803803729823608854215226233796069683774155739820425393
def continuedFra(x, y):
cF = []
while y:
cF += [x // y]
x, y = y, x % y
return cF
def Simplify(ctnf):
numerator = 0
denominator = 1
for x in ctnf[::-1]:
numerator, denominator = denominator, x * denominator + numerator
return (numerator, denominator)
def getit(c):
cf = []
for i in range(1, len(c)):
cf.append(Simplify(c[:i]))
return cf
def wienerAttack(e, n):
cf = continuedFra(e, n)
for (p2, p1) in getit(cf):
if p1 == 0:
continue
if N1 % p1 == 0 and p1 != 1:
return p1
print('not find!')
q1 = wienerAttack(N1, N2)
p1 = gmpy2.iroot(N1 // q1, 2)[0]
p2 = gmpy2.next_prime(p1)
q2 = gmpy2.next_prime(q1)
phi1 = p1 * (p1 - 1) * (q1 - 1)
phi2 = p2 * (p2 - 1) * (q2 - 1)
d1 = inverse(E1, phi1)
d2 = inverse(E2, phi2)
m1 = pow(c1, d1, N1)
m2 = pow(c2, d2, N2)
print(long_to_bytes(m1) + long_to_bytes(m2))
|
事后，计算(N1/N2-Q1/Q2) - (1/2*Q2**2)，得到结果为-6.76095158601395e+307，与理论相符
结语
希望继续坚持
想着能不能利用这个条件把
笑死 花里胡哨，一拳打死 然后就是RSA解密，和平常不同的是，
解密代码如下：
如果真的是这么解的话那就太草了，就去找了找大佬的解法，采用了连分数,低解密指数攻击原理 RSA中有一个很著名的攻击方法，低解密指数攻击，其中的代表就是wiener attack 其中就用到了连分数，具体原理网上都有，这里不再赘述 唯一令我疑惑的是，为什么可以用连分数，并且保证有解（这在很多介绍维纳攻击法的文章中是没有提到或者一笔带过的），我找到了一篇介绍wiener attack的论文，有这样一段话： 
然后我去搜了关于连分数的勒让德理论，找到了另一篇论文，给出了证明： 
关于维纳攻击法的完整推导，我打算出一期完整的博客 关于本题，由于 \[
\dfrac{N1}{N2} = \left(\dfrac{P1}{P2}\right)^{2}\left(\dfrac{Q1}{Q2}\right)
\] 又因为有