BUUCTF 每日打卡 2021-4-11
引言
终于找到虎符杯 Crypto 部分的 wp 今天来填坑
[2021 虎符杯]cubic
先上题目给的附件： 1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47from math import gcd
from functools import reduce
from fractions import Fraction as Frac
N = 6
def read_num(prompt):
try:
num = int(input(prompt))
except:
return 0
return num if num > 0 else 0
print(f"Please give me {N} pairs of positive integers (x,y,z) "
f"satisfying the equation `x/(y+z) + y/(z+x) + z/(x+y) = {N}`\n")
anss = []
mark = 0
for i in range(N):
x = read_num("[>] x: ")
y = read_num("[>] y: ")
z = read_num("[>] z: ")
if x * y * z == 0: # positive integer
mark = 1
print("This is not what i want!\n")
break
# reduce(gcd, [x, y, z]) = gcd(gcd(x,y), z)
if reduce(gcd, [x, y, z]) != 1: # (kx, ky, kz)
mark = 1
print("This is not what i want!\n")
break
if Frac(x, y+z) + Frac(y, z+x) + Frac(z, x+y) != N:
mark = 1
print("This is not what i want!\n")
break
ans = tuple(sorted([x, y, z])) # (y, x, z)
if ans in anss:
mark = 1
print("This is not what i want!\n")
break
else:
print("You are right!\n")
anss.append(ans)
if mark == 0:
flag = open('/flag', 'r').read()
print("flag is: " + flag + "\n")
else:
print("Something wrong!\n")
结果： 
啊这 当然不可能这么简单
事实上，\(\frac{x}{y+z}+\frac{y}{x+z}+\frac{z}{x+y}=4\) 的解十分复杂： 
如果能爆破出来才有问题 而这个问题可以转化成 椭圆曲线问题（跪谢 Pheonix dl 指点迷津） 这就涉及到我的知识盲区了 下午就开始学椭圆曲线 如 wp 中的论文所述 对于形如 \[
N=\frac{a}{b+c}+\frac{b}{a+c}+\frac{c}{a+b}, N \in\mathbb{N^{*}}
\] 可以转化成三元三次方程 \[
N(a+b)(b+c)(c+a)=a(a+b)(c+a)+b(b+c)(a+b)+c(c+a)(a+b)
\] 可以通过线性变换，将其转化成常见的椭圆曲线（形如 \(y ^{2} = ax ^{3}+bx ^{2}+cx+d\)）的形式： \[
y ^{2} = x ^{3}+(4N ^{2} + 12N - 3)x ^{2}+32(N+3)x
\] 其中 \[
\begin{cases}
x=\dfrac{-4(a+b+2c)(N+3)}{(2a+2b-c)+(a+b)N}\\
y=\dfrac{4(a-b)(N+3)(2N+5)}{(2a+2b-c)+(a+b)N}
\end{cases}
\] 别问，问就是数理基础 当然也可以映射回去： 设 s=a+b+c \[
\begin{cases}
\dfrac{a}{s}=\dfrac{8(N+3)-x+y}{2(4-x)(N+3)}\\
\dfrac{b}{s}=\dfrac{8(N+3)-x-y}{2(4-x)(N+3)}\\
\dfrac{c}{s}=\dfrac{-4(N+3)-(N+2)x}{(4-x)(N+3)}
\end{cases}
\] 具体怎么转化，可以参考这篇文章 这篇文章是以 \(\frac{a}{b+c}+\frac{b}{a+c}+\frac{c}{a+b}=4\) 为例 通过介绍丢番图等式： \[
P(x_{1},x_{2},\cdots,x_{k})=\sum _{ {0\leq i_{j}\leq n_{j} } }a_{ {i_{1}i_{2}\cdots i_{k} } }x_{1}^{ {i_{1} } }x_{2}^{ {i_{2}} }\cdots x_{k}^{ {i_{k} } }=0
\] 从一阶到三阶（三阶即为所求等式的转化形式）来介绍解法 这里不再赘述 其中的线性变换部分
当然，下文给出了程序解法：
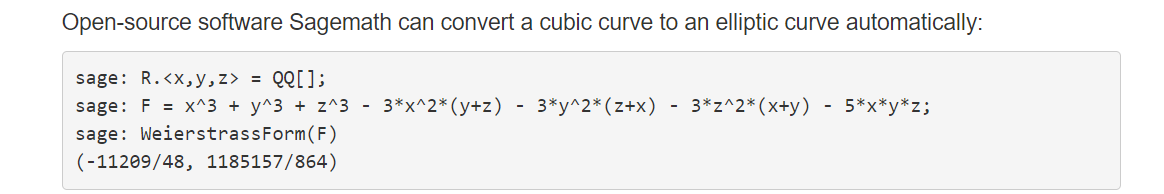数理基础不扎实的我只能代数字，套程序了
理论推导就到这里 接下来是求解 wp 中用 sagemath 封装好的椭圆曲线算法进行求解 关于椭圆曲线求解，可以参考ECC椭圆曲线加密算法：介绍 当然，这道题其实不涉及加密部分，真正的椭圆曲线加密算法复杂的多（如应用于比特币） 自己实现其实也不麻烦 这里不再赘述
最后还有个小插曲 当时题目刚出来的时候发现没有获取 flag 的方式，然后做着做着题目下线了，添了一个得到 flag 的地址 提交答案获取 flag 的部分也是 wp 中可以借鉴（抄袭）的地方
[BUU]CheckIn
附件给了一串字符：dikqTCpfRjA8fUBIMD5GNDkwMjNARkUwI0BFTg== 看到后面两个 “==” 大概率是 base64 随便找了个网站解密 
这是什么玩意？ 还有替换密码？ 拿去爆破 
只好找 wp ，得知要拿 base64 解码出来的结果 rot 解密 解密结果以及 rot-N 加密原理如下： 
rot-N 加密解密网站：https://www.qqxiuzi.cn/bianma/ROT5-13-18-47.php
结语
搞了一上午 虎符那题的文献其实比赛的时候找到了，但是没有照算法实现，而是选择先去学椭圆曲线加密算法，是我的一大失误 今天就水到这，希望继续坚持