Σ2333! の 博客
0%

发表于 更新于

BUUCTF 每日打卡 2021-4-30

引言

啊 五一假期开始了

坏蛋是雷宾

题目描述如下： 在这里插入图片描述 看到校验码，想起之前一个奇偶校验位的题 但是好像行不通 只能找 wp 得知是 RSA 衍生算法——Rabin 算法 在这里插入图片描述 wp 中没有采用原始的攻击方法 而是采用下面的方法 在这里插入图片描述 如果把 wp 中的代码放到 python3 中运行会报错： TypeError: pow() 3rd argument not allowed unless all arguments are integers 应该为：

1
2
3
# p = q = 3 (mod 4)
mp = pow(c, (p + 1) // 4, p)
mq = pow(c, (q + 1) // 4, q)

另一处值得注意的地方是：

1
2
inv_p = invert(p, q)
inv_q = invert(q, p)

没有采用扩展欧几里得求 \(y_{p},y_{q}\) ，而是采用求逆元的方法 原理是： 由于 \[ y_{p} * p + y_{q} * q = 1 \] 所以两边分别对 \(p, q\) 取模 可得 \[ \begin{cases} y_{p}*q \equiv 1\space (mod \space p)\\ y_{q}*p \equiv 1\space (mod \space q) \end{cases} \] 直接用 gmpy2 库中的 gcdext() 方法实现扩展欧几里得算法的代码如下： 

1
2
3
import gmpy2

g, yp, yq = gmpy2.gcdext(p, q)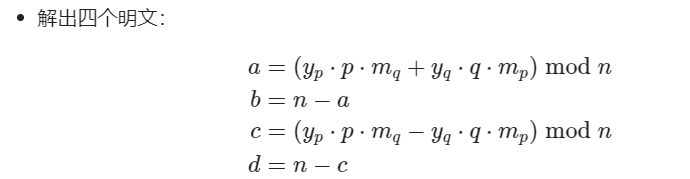
下一步： 在这里插入图片描述 根据题目描述：密文是162853095，校验码二进制值是110001，根据说明是放在明文后一起加密的，明文与密文长度相同。 从四个明文中找到正确的明文 完整代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
import gmpy2

n = 523798549
p = 10663
q = 49123
c = 162853095
# p = q = 3 (mod 4)
mp = pow(c, (p + 1) // 4, p)
mq = pow(c, (q + 1) // 4, q)

g, yp, yq = gmpy2.gcdext(p, q)

a = (yp * p * mq + yq * q * mp) % n
b = n - a
c = (yp * p * mq - yq * q * mp) % n
d = n - c

check = '110001'
for i in [a, b, c, d]:
    if bin(i)[2:][-len(check):] == check:
        print(i)
        m = i
print(int(bin(m)[2:][:-len(check)], 2))

n 可以直接爆破，这里不再赘述 最后得到的 m，MD5 加密 结果如下： 在这里插入图片描述 哈希值即为 flag

结语

累了累了 还是好好享受假期吧 希望继续坚持