BUUCTF 每日打卡 2021-9-5

## 引言

假期的最后一天（其实已经是到学校的第二天了），明天就要开始上课了今天打了打 GrabCON CTF2021

[GrabCON CTF2021]Warm-up

题目附件如下：

S01ZRENXU1NJVkhGUVZKUkpaRkZNMlNLSTVKVENWU0xLVlZYQVlLVElaTkVVVlRNS0pIRkc2U1dKVkpHV01LWEtaQ1VVVENXTlJORlNVS1dOUkdGS01EVUs1S0dXVlNLS1pDWFFUQ1ROUllFT1VUTE1STFZDTUxFSk5MR1c0Q0lLWVlEQ1RDWEtWMkZNVjJWTkJKRk1SS09MQktHV05EWktKV0U0VlNOTlJTRVdWVEtLSkxWR01CUklOTEdXNUNQS05XRkVSQ1dLWkhFSVVaUk9CTUZFMjJXS1ZKVENXU0tLWlZWVVJTVUdGTEZLVkNGR0ZIVTRSU1ZQRkdXWVRTTUtOVlRLVEtTR0ZSVEFVSlFNUkdGSVZUTUs1SkZNVExaS1pWWElWMk5OTkxFNFZUS0pKTFZJUkxRSlZKR1dNS1RLTVlEU1RDVk5OMkVRVjJXSlpLRk1WTFVKTkpUQ1VTRUtaV0U0VjJTR0JORklVU1dNUkxGTVJMVUpSSldXNkNYS0lZVlVSQ1RHQVlVT1ZDRk1STUU0VktPS0ZKVENTU0VLWldGTVZLUkdGU0U2VkxMTVJNVktNS1dNRktXV09LREtFWUZVVUNWTk4yRVFVWlJPQkdGTVJLT0s1S1RBM0NNS0pWWFFTQ1hLWlNFSVZMTE1SRFZJMjIySlJMR1dUU0hLSVlWVVMyV05OU0ZHVTMySkpGRksyM0VLVklWTVVTVUtSS1hJVDJXR0JORk1WTDJKSk1GRU1DMktOTEVLUlNXS05XRU1VQ1JOTlNFT1ZEMkpGNUZPVkxMR0ZKVEFXU09LWVlVNFJTVEdGWUVJVlJRTlJKRTIyWlZKNUtHV05LR0tWTEZVVkNXTk00VUdVM0xMSkZGSzIzWUtKSldXU1NMS0lZV0dNS1JHRkpFWVZMTEpaTVZLVlNPSlJLVEE1Q1NLNUtWRVZDV0tWSEZNVVJRSVVZRk0yMkdLWkpXVVZTSktaS0RBT0tRS1FZRFNVQ1JIVTZRPT09PQ==

容易猜测是base64，找了个base64在线工具，解密结果如下：

联系题面，不难猜想解密结果为base32加密密文，又找了一个base32在线解密工具，解密结果如下：

容易发现，解密结果又是base64密文形式，接着连续base64和base32解密，得到结果：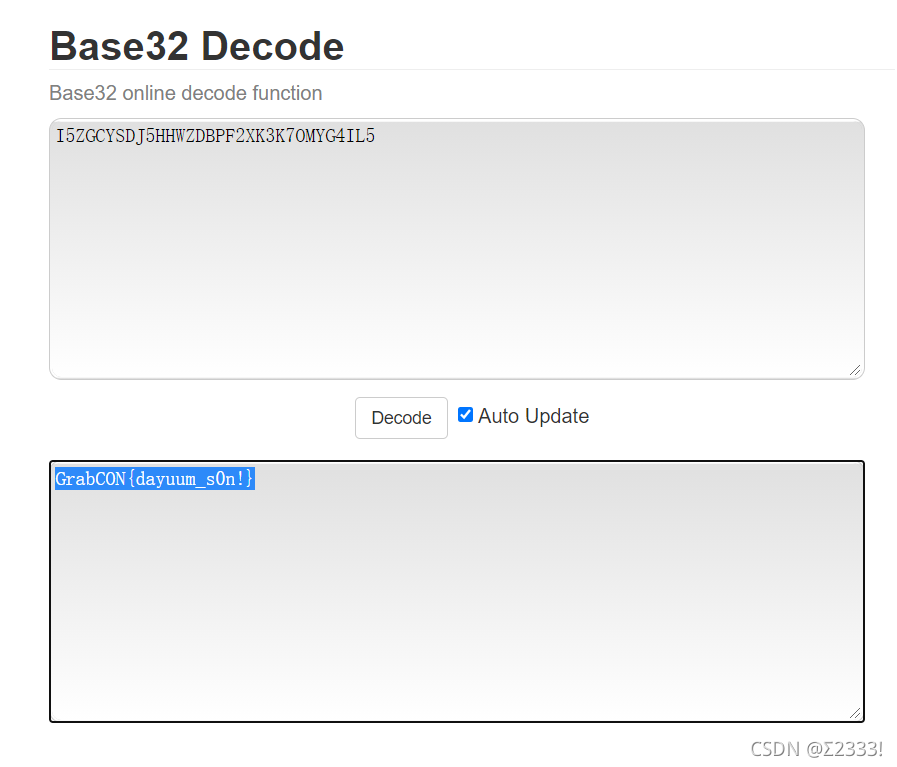

[GrabCON CTF2021]Poke Ball RSA

附件内容如下：

1
2
3

n = 498934084350094415783044823223130007435556803301613073259727203199325937230080661117917023582579699673759861892703348357714077684549303787581429366922208568924252052118455313229534699860304480039147103608782140303489222166267907007839021544433148286217133494762766492655602977085105487216032806292874190551319
e = 134901827939710543990222584187396847806193644190423846456160711527109836908087675183249532946675670587286594441908191054495871501233678465783530503352727362726294270065122447852357566161748618195216611965946646411519602447104878893524856862722902833460104389620397589021732407447981724307130484482495521398799
c = 100132888193232309251839777842498074992587507373917163874335385921940537055226546911990198769720313749286675018486390873216490470403470144298153410686092752282228631590006943913867497072931343354481759219425807850047083814816718302223434388744485547550941814186146959750515114700335721173624212499886218608818

e很长，盲猜wiener's attack，套用网上抄的代码如下：

import gmpy2
from Crypto.Util.number import *

def transform(x, y):  # 使用辗转相处将分数 x/y 转为连分数的形式
    res = []
    while y:
        res.append(x // y)
        x, y = y, x % y
    return res


def continued_fraction(sub_res):
    numerator, denominator = 1, 0
    for i in sub_res[::-1]:  # 从sublist的后面往前循环
        denominator, numerator = numerator, i * numerator + denominator
    return denominator, numerator  # 得到渐进分数的分母和分子，并返回


# 求解每个渐进分数
def sub_fraction(x, y):
    res = transform(x, y)
    res = list(map(continued_fraction, (res[0:i] for i in range(1, len(res)))))  # 将连分数的结果逐一截取以求渐进分数
    return res


def get_pq(a, b, c):  # 由p+q和pq的值通过维达定理来求解p和q
    par = gmpy2.isqrt(b * b - 4 * a * c)  # 由上述可得，开根号一定是整数，因为有解
    x1, x2 = (-b + par) // (2 * a), (-b - par) // (2 * a)
    return x1, x2


def wienerAttack(e, n):
    for (d, k) in sub_fraction(e, n):  # 用一个for循环来注意试探e/n的连续函数的渐进分数，直到找到一个满足条件的渐进分数
        if k == 0:  # 可能会出现连分数的第一个为0的情况，排除
            continue
        if (e * d - 1) % k != 0:  # ed=1 (mod φ(n)) 因此如果找到了d的话，(ed-1)会整除φ(n),也就是存在k使得(e*d-1)//k=φ(n)
            continue

        phi = (e * d - 1) // k  # 这个结果就是 φ(n)
        px, qy = get_pq(1, n - phi + 1, n)
        if px * qy == n:
            p, q = abs(int(px)), abs(int(qy))  # 可能会得到两个负数，负负得正未尝不会出现
            d = gmpy2.invert(e, (p - 1) * (q - 1))  # 求ed=1 (mod  φ(n))的结果，也就是e关于 φ(n)的乘法逆元d
            return d
    print("该方法不适用")


n = 498934084350094415783044823223130007435556803301613073259727203199325937230080661117917023582579699673759861892703348357714077684549303787581429366922208568924252052118455313229534699860304480039147103608782140303489222166267907007839021544433148286217133494762766492655602977085105487216032806292874190551319
e = 134901827939710543990222584187396847806193644190423846456160711527109836908087675183249532946675670587286594441908191054495871501233678465783530503352727362726294270065122447852357566161748618195216611965946646411519602447104878893524856862722902833460104389620397589021732407447981724307130484482495521398799
c = 100132888193232309251839777842498074992587507373917163874335385921940537055226546911990198769720313749286675018486390873216490470403470144298153410686092752282228631590006943913867497072931343354481759219425807850047083814816718302223434388744485547550941814186146959750515114700335721173624212499886218608818
d = wienerAttack(e, n)
print("d=", d)
m = pow(c, d, n)
print(long_to_bytes(m))

得到结果如下：得到e=2，原本以为是rabin 但是分解n发现： p,q都比c大，所以\(c^2 << pq=n\)，直接开根就行，结果为：

[GrabCON CTF2021]Old Monk's Password

加密代码如下：

enc = b'\x0cYUV\x02\x13\x16\x1a\x01\x04\x05C\x00\twcx|z(((%.)=K%(>'
enc1 = b'\x0bPPS\r\x0b\x02\x0f\x12\r\x03_G\t\x08yb}v+--*+*8=W,>'
enc2 = b'\x07A[\x06\\\r\x15\t\x04\x07\x18VG]U]@\x02\x08&9&%\' 41".;'

import codecs
import random

class pass_w:
    x = "hjlgyjgyj10hadanvbwdmkw00OUONBADANKHM;IMMBMZCNihaillm"
    def encode(self, text, i = -1):
        

        if i < 0 or i > len(self.x) + 1:
            i = random.randint(0, len(self.x) + 1)

        out = chr(i)
        for c in text:
            out += chr(ord(c) ^ ord(self.x[i]))
            i = (i + 1)%79                 

        return codecs.encode(out)
    

y = pass_w()
print(y.encode("REDACTED"))


#Enclose password within GrabCON{}

按照加密代码，密文的第一位即为随机数i，然后按照加密代码逐位异或运算即可，解密代码为：

enc = b'\x0cYUV\x02\x13\x16\x1a\x01\x04\x05C\x00\twcx|z(((%.)=K%(>'
enc1 = b'\x0bPPS\r\x0b\x02\x0f\x12\r\x03_G\t\x08yb}v+--*+*8=W,>'
enc2 = b'\x07A[\x06\\\r\x15\t\x04\x07\x18VG]U]@\x02\x08&9&%\' 41".;'
def decode(cipher):
    x = "hjlgyjgyj10hadanvbwdmkw00OUONBADANKHM;IMMBMZCNihaillm"
    i = cipher[0]
    m = ''
    for c in cipher[1:]:
        m += chr(c ^ ord(x[i]))
        i = (i + 1) % 79
    return m
print(decode(enc) + decode(enc1) + decode(enc2))
print('GrabCON{' + decode(enc) + '}')

发现三个密文的明文都是一样的，结果为：

结语

可能要摸一段时间希望继续坚持

Σ2333! の博客

未命名

BUUCTF 每日打卡 2021-9-5

[GrabCON CTF2021]Warm-up

[GrabCON CTF2021]Poke Ball RSA

[GrabCON CTF2021]Old Monk's Password

结语